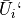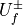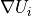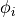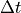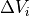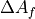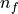Developer Guide

Overview of Code Structure

Start

pyBaram can be executed using the command pybaram which is linked to __main__.py. In run or restart modes, the command calls process_common in the pybaram.api.simulation. module. Here, the integrator object is initiated, and the run method is called to conduct the simulation.

Integrators

The Integrator object conducts time integration of the discretized equations. When the integrator is initiated, it invokes the system class in the pybaram.solvers module to compute the right-hand side term of the FVM. Additionally, plugins are invoked by this integrator object for post-processing.

pybaram can conduct both steady and unsteady simulations, and they are implemented in the pybaram.integrators.steady and the pybaram.integrators.unsteady modules, respectively. Here, the construct_stage method generates the kernels for time integration. For unsteady simulation, explicit Runge-Kutta schemes can be applied, as implemented below.

TVD-RK3

class pybaram.integrators.unsteady.TVDRK3(be, cfg, msh, soln, comm)

_dt_cfl(ttag)

_make_stages(out, *args)

add_tlist(dt)

advance_to(ttag)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'none'

mode = 'unsteady'

name = 'tvd-rk3'

nreg = 3

run()

step(dt, t)

For steady simulation, either explicit Runge-Kutta schemes or implicit LU-SGS schemes can be used, as implemented below.

5-stage Runge-Kutta

class pybaram.integrators.steady.FiveStageRK(be, cfg, msh, soln, comm)

Jameson Multistage scheme ref : Blazek book 6.1.1 (Table 6.1)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'none'

mode = 'steady'

name = 'rk5'

nreg = 3

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

LU-SGS

class pybaram.integrators.steady.LUSGS(be, cfg, msh, soln, comm)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'spectral-radius'

mode = 'steady'

name = 'lu-sgs'

nreg = 3

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

Colored LU-SGS

class pybaram.integrators.steady.ColoredLUSGS(be, cfg, msh, soln, comm)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'spectral-radius'

mode = 'steady'

name = 'colored-lu-sgs'

nreg = 3

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

Block Jacobi

class pybaram.integrators.steady.BlockJacobi(be, cfg, msh, soln, comm)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'approx-jacobian'

mode = 'steady'

name = 'jacobi'

nreg = 4

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

Block LU-SGS

class pybaram.integrators.steady.BlockLUSGS(be, cfg, msh, soln, comm)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'approx-jacobian'

mode = 'steady'

name = 'blu-sgs'

nreg = 3

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

Colored Block LU-SGS

class pybaram.integrators.steady.ColoredBlockLUSGS(be, cfg, msh, soln, comm)

property _cfl

_local_dt()

_make_stages(out, *args)

advance_to()

complete_step(resid)

construct_stages()

property curr_aux

property curr_mu

property curr_soln

impl_op = 'approx-jacobian'

mode = 'steady'

name = 'colored-blu-sgs'

nreg = 3

print_res(residual)

rhs(idx_in=0, idx_out=1, is_norm=False)

run()

step()

The hierarchy of integrator class can be shown as below.

Solvers

In the pybaram.solvers module, the governing equations and their spatial discretizations are implemented. For each submodule corresponding to governing equations, there are objects such as system, elements, inters and vertex.

System

The system object, invoked from the integrator, initializes elements, inters and vertex objects by reading mesh and restarted solution, if available. These objects have a construct_kernels method to generate kernels for computing the right-hand side. Here, the rhside method schedules these kernels. To enhance efficiency, non-blocking communications and computations are overlapped. The class hierarchy of the system can be depicted as follows:

• BaseSystem : initiates objects and generates kernels from these object

• BaseAdvecSystem : rhside method for advection problems, such as Euler systems.

  rhside for advection

  BaseAdvecSystem.rhside(idx_in=0, idx_out=1, t=0, is_norm=False)

• BaseAdvecSystem : rhside method for advection-diffusion problems, such as Navier-Stokes system.

  rhside for advection-diffusion

  BaseAdvecDiffSystem.rhside(idx_in=0, idx_out=1, t=0, is_norm=False)

• RANSSystem : initiates objects and generates kernels from these object for RANS simulation

Elements

The elemenets object stores solution and other arrays. It also generates kernels, looping over elements. The class hierarchy can be depicted as follows:

• BaseElements : defines geometry and related properties

• BaseAdvecElements : common kernels for finite volume method, allocation of arrays

• EulerElements : specific kernels for Euler equations

• NavierStokesElements : specific kernels for Navier-Stokes equations

• FluidElements : physics of compressible inviscid flow

• ViscousFluidElements : physics of viscous flow

For RANS simulation, class hierarchy can be depicted as follows:

• RANSElements : common kernels for RANS computation

• RANSSAElements : specific kernels for Spalart-Allmaras turbulence model

• RANSKWSSTElements : specific kernels for SST turbulence model

• RANSSAFluidElements : physics of Spalart-Allmaras turbulence model

• RANSKWSSTFluidElements : physics of SST turbulence model

Inters

The inters objects generate kernels looping over interfaces. There are three types of interfaces: Internal, boundary, and MPI interfaces. The abstract classes for them can be depicted as follows:

• BaseInters : computes geometrical properties and defines view to refer array in elements

• BaseIntInters : abstract class for internal interface

• BaseBCInters : abstract class for physical boundary interface

• BaseMPIInters : abstract class for MPI boundary interface

The class hierarchy of internal interfaces can be depicted as follows:

• BaseAdvecIntInters : common kernel to compute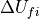

• BaseAdvecDiffIntInters : common kernel to compute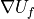

• EulerIntInters : kerenl to compute inviscid flux

• NavierStokesIntInters : kerenl to compute viscous flux

• RANSIntInters : kernel to compute RANS flux

• RANSSAInters : kernel to compute turbulent flux for Spalart-Allmaras turbulence model

• RANSKWSSTInters : kernel to compute turbulent flux for SST turbulence model

The class hierarchy of physical boundary interfaces can be depicted as follows:

The overall structure and role of these classes are the same as internal interfaces. The construct_bc method in BaseAdvecInters compiles the boundary condition function, and specific formulations are implemented in this class. For example, the hierarchy of boundary conditions for Euler equations can be depicted as follows:

The class hierarchy of MPI interfaces can be depicted as follows:

The overall structure and role of these class are the same as internal interfaces. MPI communication kernels are defined in BaseAdvecMPIInters.

Vertex

The vertex object generates kernel looping over vertex. The class hierarchy can be depicted as follows:

• BaseVertex : view to refer array in elements

• BaseVertex : kernel to find extreme values at vertex

Plugins

The plugin modules handle the post-processing after each iteration or a fixed number of iterations. The class hierarchy can be depicted as follows:

• StatsPlugin : collect statistics (time step or residual)

• WriterPlugin : write output file

• ForcePlugin : compute aerodynamic force coefficients

• SurfIntPlugin : compute integrated and averaged properties over boundary surface.

Backends

The pybaram.backends module accelerates the pure Python loop and manages the execution of kernels. Currently, only the CPUBackend is implemented for serial and parallel computation using CPU. This module provides two main features; generating kernels and handling data types for executions.

Compile Kernel

In the integrators and the solvers modules, pure Python functions are defined. These functions are compiled as kernels using loop generators in the pybaram.backends.cpu.loops module. The Numba JIT compiler is then called, and the pure Python functions are compiled to construct serial or parallel loops.

Data Types for Execution

Currently, four data types are defined in the pybaram.backends.types.

class pybaram.backends.types.ArrayBank(mat, idx)

ArrayBank object

It stores list of arrays and point one of them.

class pybaram.backends.types.Kernel(fun, *args, arg_trans_pos=False)

Kernel object

It stores the static arguments. It executes function with static and dynamic arguments

class pybaram.backends.types.MetaKernel(kerns)

Meta kernel object

It stores series of kernels and run all them.

class pybaram.backends.types.Queue

Simple Queue

It collects MPI requests and synchronizes all these commnunications.

Variables

The name of the variable pyBaram may seem somewhat condensed. The table below provides a summary of mathematical symbols and the corresponding meanings of major arrays:

Notation of Variables in pyBaram

Name	Symbol	Meaning	N/A
upts		array of cell-averaged state variable vector
fpts		array of state vectors at faces
grad		array of gradient of the state variables
lim		array of slope limiter
dt		array of time step size
vpts		array of minimum and maximum at each vertex
vol		array of volume of cell
mag_snorm		array of area of face
vec_snorm		array of unit normal vector of face

Code Snippets Analysis

Here, the methods for generating kernels and constructing MPI communications are explained with two sample code snippets.

Inviscid Flux Kernel

In pybaram.backends.cpu.loop module, there are two methods: make_serial_loop1d and make_parallel_loop1d. These methods generate an accelerated kernel from a Python function. A function written in pure Python is compiled using just-in-time compilation with Numba. When make_parallel_loop1d is used, each thread parallelly executes the loop of this compiled function. Otherwise, the loop of the compiled function is executed sequentially.

pybaram.backends.cpu.loop.make_parallel_loop1d(ne, func, n0=0)

pybaram.backends.cpu.loop.make_serial_loop1d(ne, func, n0=0, debug=False)

As an example, let’s consider the comm_flux function. The EulerIntInters class in the pybaram.solvers.euler.inters module has _make_flux method, which generates the kernel to compute numerical flux. The comm_flux function utilizes a plain for loop structure, which is more similar to the loop structure of C/C++ or Fortran than a Pythonic-style one. Therefore, one can readily adopt a well-developed function from a legacy solver into pyBaram. The allocation of local arrays was hoisted due to limited functionalities for developing local static variables in Numba. Furthermore, the _make_flux method passes this Python function to the make_serial_loop1d or make_parallel_loop1d method of the backend object and finally returns the serialized or parallelized kernel, respectively.

class pybaram.solvers.euler.inters.EulerIntInters(be, cfg, elemap, lhs, rhs)

_make_flux()

The generated kernel is constructed by construct_kernels method of BaseAdvecIntInters in pybaram.solvers.baseadvec. When this kernel is called, the reconstructed values at the face 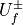is used as static argument. Thus, Kernel data type binds this compiled kernel and the static arguments. When Kernel object is called, dynamic arguments can be also provided. All arguments are parsed, then the compiled kernel is executed.

class pybaram.solvers.euler.inters.BaseAdvecIntInters(be, cfg, elemap, lhs, rhs)

construct_kernels()

Non-blocking Send/Receive

pyBaram exploits the mpi4py ppackage for MPI communication. Non-blocking communications are employed and overlapped with computing kernels. These methods are implemented in the MPIInters class.

In the construct_kernels method, non-blocking send and receive kernels, along with their requests, are constructed using the _make_send and _make_recv methods. Buffers are passed to these methods, and the _sendrecv` method is invoked. In this method, the start function is returned. When this function is called with a Queue instance in rhside, the MPI request for this communication is registered in the Queue instance, and the non-blocking communication starts. This communication is finalized when the sync method in the Queue instance is called.

class pybaram.solvers.baseadvec.inters.BaseAdvecMPIInters(be, cfg, elemap, lhs, dest)

construct_kernels()

_sendrecv()

_make_send()

_make_recv()

class pybaram.backends.types.Queue

Simple Queue

It collects MPI requests and synchronizes all these commnunications.

register()

sync()